本記事は、研究者が自ら著書の論文を解説する特別企画です。
Xにて企画への応募を募集したところ、何名かの方からご連絡をいただき、今回初の公開となりました。
今回は、NECの宮川大輝氏による、”Toward Equation of Motion for Deep Neural Networks: Continuous-time Gradient Descent and Discretization Error Analysis”の解説です。
なお、本企画は継続開催中です。研究者の方はこちらからご応募ください。
参照論文情報
- タイトル:Toward Equation of Motion for Deep Neural Networks: Continuous-time Gradient Descent and Discretization Error Analysis
- 著者:Taiki Miyagawa
- 所属:NEC Corporation, Japan
- URL:https://doi.org/10.48550/arXiv.2210.15898
- 備考:NeurIPS 2022採択
以下、ご本人による寄稿です。普段とは一味違ったスタイルと内容をぜひお楽しみください。
研究者情報
名前
宮川大輝(Miyagawa Taiki)
X (旧Twitter): https://twitter.com/kanaheinousagi
Google Scholar: https://scholar.google.com/citations?user=wzVtu1cAAAAJ&hl=ja
Semantic Scholar: https://www.semanticscholar.org/author/Taiki-Miyagawa/102939912
(実は1000本以上の論文を紹介している匿名のTwitterアカウントもあります)
所属
- ~2017年
- 京都大学 素粒子論研究室
- 2017年~現在
- NEC Corporation
- 2018~2022年
- 理研AIP
- 2023年~現在
- Independent researcher (野良研究者) としても論文投稿中
経歴
「物質の最小構成要素の研究(素粒子物理学)」から「深層学習理論」へ鞍替え。
現在「物理学×深層学習」&「深層学習×物理学」の研究中。
主な論文:
- “Sequential Density Ratio Estimation for Simultaneous Optimization of Speed and Accuracy”
- ICLR 2021 Spotlight
- Akinori F. Ebihara, Taiki Miyagawa, Kazuyuki Sakurai, Hitoshi Imaoka
- https://arxiv.org/abs/2006.05587
- “The Power of Log-Sum-Exp: Sequential Density Ratio Matrix Estimation for Speed-Accuracy Optimization”
- ICML 2021
- Taiki Miyagawa, Akinori F. Ebihara
- https://arxiv.org/abs/2105.13636
- “Toward Equation of Motion for Deep Neural Networks: Continuous-time Gradient Descent and Discretization Error Analysis”
- NeurIPS 2022
- Taiki Miyagawa
- https://arxiv.org/abs/2210.15898
- “Toward Asymptotic Optimality: Sequential Unsupervised Regression of Density Ratio for Early Classification”
- ICASSP 2023
- Akinori F. Ebihara, Taiki Miyagawa, Kazuyuki Sakurai, Hitoshi Imaoka
- https://arxiv.org/abs/2302.09810
など。
本研究に取り組んだ動機
「物理学の知見から、深層ニューラルネットワークの学習過程(超複雑!)を説明できるだろうか?」という素朴な疑問から発生した研究です。この根源的な問題に対し、部分的に解答を見出すことに成功しました。
今回紹介させていただく研究は、「深層学習の学習過程」という深遠な謎に理論的に取り組むお話です。これを大学学部生でもザックリ理解できるように簡易化してお伝えします(逆に専門家の方は、予めこの点をご了承ください)。普段AIDBで取り上げられる研究とはやや毛色の違うお話かもしれません。しかしこの記事を読み終える頃には、皆さんの知的好奇心は満ちていることでしょう。
研究内容の紹介
研究全体を端的に言うとどんなものか
深層ニューラルネットワークの運動方程式を導出しました。
これは一体どういう意味なのか?
以下で説明します。
背景
運動方程式とは何か?
運動方程式は物理学における専門用語です。
物理学とは、数学という言語を用いて自然現象を説明・予言する学問体系です。
対象となる物理系を説明できる微分方程式を構築し、解く。
それが物理学者のお仕事です。
その微分方程式を総称して「運動方程式」といいます。
ニュートンの運動方程式 ma = F やシュレディンガー方程式といった運動方程式は、皆さん耳馴染みがあるかもしれません(図1)。

NeurIPS 2022の発表で流した自作アニメのワンシーンです。
深層ニューラルネットワークの運動方程式とは何か?
それでは、「深層ニューラルネットワークの」運動方程式とは何でしょうか?つまり、
深層ニューラルネットワークの学習過程を説明できる微分方程式はどのようなものでしょうか?
実は、これは既にいくつか知られています。勾配流(gradient flow)やランジュバン方程式(stochastic differential equation)がそれに当たります。
これらの微分方程式は勾配法や確率的勾配法(SGD)を直接扱うよりも使い勝手が良く、実際にこれらを使って勾配法や確率的勾配法の収束の早さを調べる研究が山ほどあります。
運動方程式完成……?
では深層ニューラルネットワークの運動方程式は既に完成しているのでしょうか?
答えは No です。
実はこれらの微分方程式には大きな欠点があります。それは、
「学習率が非常に小さい場合しか学習過程を説明できない」
ことです。
これは微分の定義を思い出すとすぐに分かります。
高校数学で習うことですが、微分は、
においてεを非常に小さくすることで定義されています。上述の微分方程式では、εに対応する量として学習率を用いています。
したがって、上述の微分方程式は、学習率が0の極限でないと成立しない微分方程式なのです。実際には、0.01といった有限の大きさの学習率を使う事でしょう。これでは現実の深層ニューラルネットワークの学習過程とは乖離が生じてしまいますね(図2)。
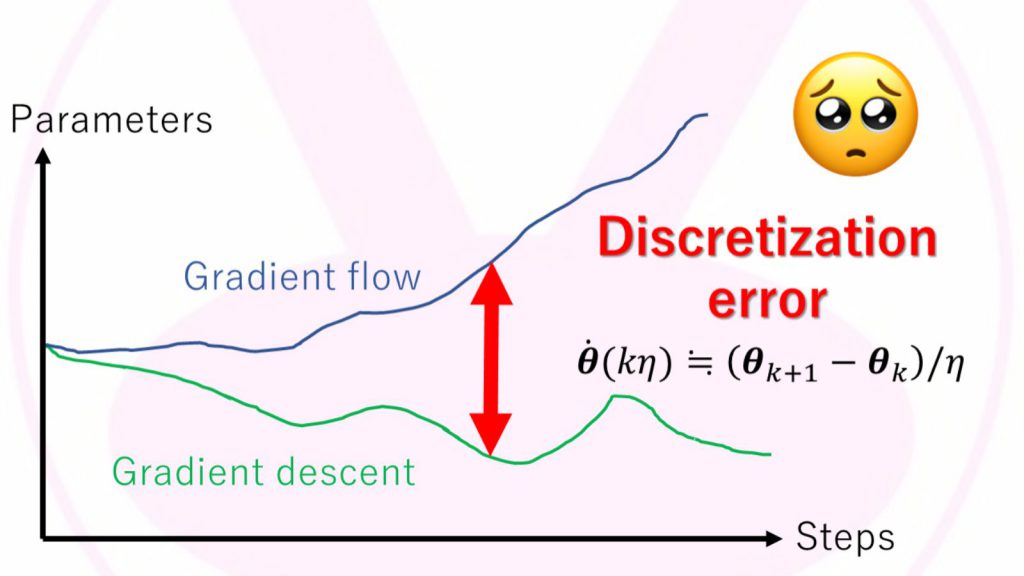
図2:勾配法(gradient descent)と勾配流(gradient flow)の間の誤差。
学習率(図中η)が無限小の極限でしか、両者は一致しないのです。
縦軸は深層ニューラルネットワークの重みパラメタの値を簡単のため1次元にしたものです。横軸は学習のステップ数です。
さて、この乖離をどのようにして埋めれば良いのでしょうか?そしてこの乖離を埋められれば、深層学習ニューラルネットワークの運動方程式が完成するのではないでしょうか?
それを実現したのが本研究なのです。
方法
ではどのようにしてこの乖離を埋めたのでしょうか。
ヒントは
微分方程式の数値シミュレーション理論
にありました。微分方程式の数値シミュレーションでは、0の極限はコンピューター上で扱えないので、微分を有限のϵで近似計算する必要があります(有限差分法)。この近似による誤差を離散化誤差とここでは呼びます(図2)。その離散化誤差を打ち消す研究が長年に渡って積み重なってきていました。詳細は省略しますが、この離散化誤差を打ち消す項を上述の勾配流に導入することで、深層ニューラルネットワークの学習過程を一切の誤差無しに説明できる微分方程式、すなわち深層ニューラルネットワークの運動方程式を導出することに成功したのです(図3)。
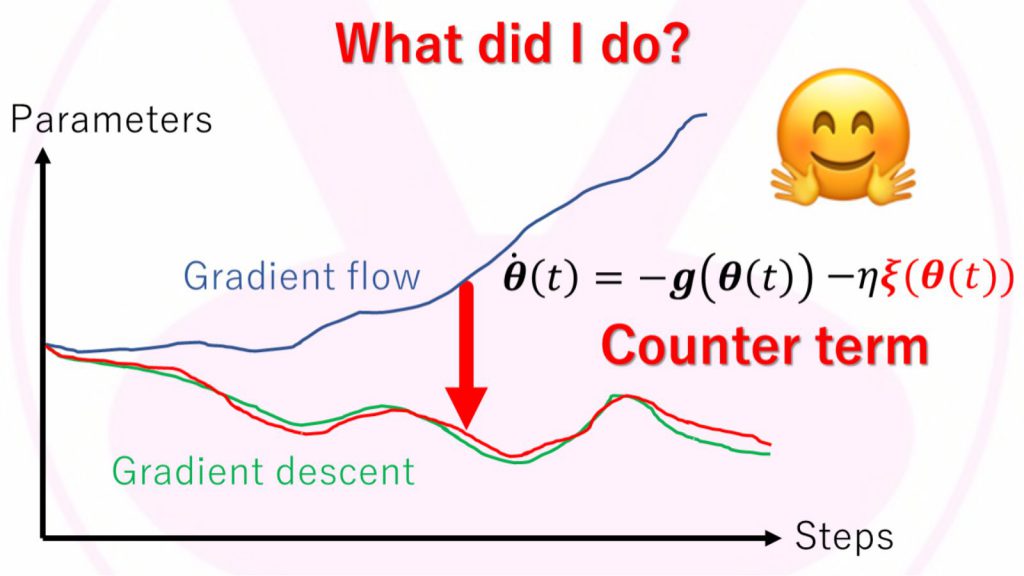
図3:深層ニューラルネットワーク(勾配法)の運動方程式。
図中のξ(θ(t))が、「離散化誤差を打ち消す項」です。
具体的な数式は複雑なので省略してあります。
実験による理論の検証
ここまでの話では完全に数学の話しかしていませんでした。果たして運動方程式は実際の学習過程を正確に説明できているのでしょうか?はたまた机上の空論で終わってしまうのでしょうか?ここでは、運動方程式がいかに精度良く学習過程を説明・予言できるかを示す実験結果を、ごく一部ではありますが、一つだけお見せすることとしましょう。
少々数字が多いですが、以下の表1をご覧ください。これは深層ニューラルネットワーク内のある層の「重みパラメタのノルムの時間変化率」(注)を測ったものです。
この表を見ると、勾配流の予測結果よりも、運動方程式の予測結果の方が、実際の実験結果をすさまじい精度で予言できていることがわかりますね(たった0.0000005の違いすら見逃していません!)。
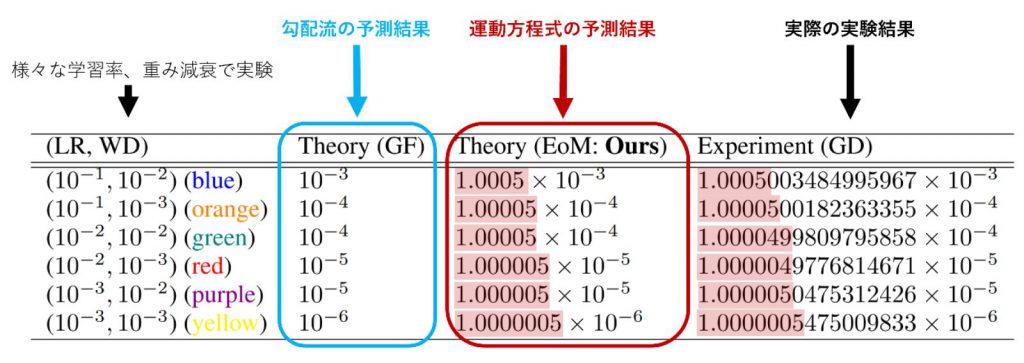
表1:Softmax層前の線形層のノルムの時間変化率。
ちなみに運動方程式には離散化誤差を打ち消す項を一部しか入れていません。
もっと項を入れると、もっと精度よく実際の実験結果と一致する事でしょう。
※注:何故突然「重みパラメタのノルムの時間変化率」なんてそんなまどろっこしい量を測り始めたのか?と疑問に思う方もいるかもしれません。それはなぜかというと、そもそも「学習過程を説明できる」とは、「深層ニューラルネットワークの超高次元の重みベクトルの時間発展を完全に予言できること」を意味するのですが、しかし超高次元の重みベクトルを二次元のブログ記事に表示するのは至難の業だからです。ですので、ここでは表と数値だけで説明できる簡単な実験結果だけを載せてあります。
まとめと展望
かくして深層ニューラルネットワークの運動方程式が構築されました。この運動方程式を用いることで、いままでブラックボックスであると言われてきた深層ニューラルネットワークの学習過程を詳らかにする用意ができたといえます。
また、本研究は更なる後続研究をいくつも生み出す可能性を秘めており、新たな論文ネタとしても手頃かつホットトピックなのでオススメです。
例えば、以上の解析では勾配法を対象にしているのですが、これを他の最適化アルゴリズムへと拡張することが考えられます。論文中でもヒントを挙げていますが、確率的勾配法やAdamといったよく使われるアルゴリズムへの拡張が比較的簡単かもしれません。深層学習理論・最適化・微分方程式等に興味のある方はぜひ試みてください。
今後取り組む予定の研究
「物理学×深層学習 & 深層学習×物理学」は、まだまだまだまだ噛めば噛むほど味がします。今回紹介した研究とは別に、私が今取り組んでいるのは、
①100年に渡り解けなかった微分方程式を機械学習の力で解く事
②深層ニューラルネットワークの熱力学を構築する事
です。
専門家の方々向けに言い換えると、
①計算量の問題で長年解けなかった数々の汎関数微分方程式を physics-informed neural network の力で解く事
②深層ニューラルネットワークの確率的勾配法 (SGD) と小さな系の熱力学 (stochastic thermodynamics) とを融合した理論体系を構築し、実用に資する知見を発見する事
です。
①は流体力学や量子力学分野の物理学者たちの長年の悲願です。
また②が完成すれば、小さな系の熱力学における長年の知見を、深層学習の学習過程の解析に輸入できるようになります。例えば、水面に浮いた花粉の運動が深層ニューラルネットワークの学習過程に似ていたりするのです。
ちなみに会社での研究では、
- 時系列早押し問題 (early classification)、
- ディープフェイク検出 (DeepFake detection)、
- 連合学習(federated learning)、
- 敵対的攻撃 (adversarial example)、
- 合成画像検出 (morphing detection)、
- 安全なLLM運用 (secure LLM)、
- プロンプトチューニング (prompt tuning)、
- 多物体追跡 (multi-object detection)、
- 顔照合 (face recognition)、
- 薬効予測、
- クラス不均衡問題 (class-imbalance problem)
といった幅広い研究を行っています。
今後もTwitterアカウントを中心に発信していくのでお楽しみに。

図4:宮川大輝のTwitterアイコン(https://twitter.com/kanaheinousagi)。
学会の発表資料等での顔出しはめったにしていません。
会社でも外でも大体このマークでやっています。
特に理由はありません。その方が面白そうだからです。
編集部後記:
深層学習の学習プロセスを運動方程式で表現するという非常に難解で複雑な問いに取り組んだ研究、とても面白く読ませていただきました。精度がきわめて高いことが特に驚きでした。
今後取り組む予定の研究に関しても、かなり興味深いですね!「100年に渡り解けなかった微分方程式を機械学習の力で解く」、とても楽しみです。
また、研究を行っているご本人による解説ならではの臨場感があり、またポイントが整理されており、読みやすいなあと感じました。
宮川さん、ご寄稿ありがとうございました!これからもよろしくお願いします。
なお、冒頭にも述べましたが、本企画(研究者が自ら著書の論文を解説する特別企画)は継続開催中です。研究者の方はこちらからご応募ください。







