こんにちは、じゅんペー(@jp_aiboom)です！

僕は現在東京大学の理系の二年生です。この連載では、AI初心者の僕が、「パターン認識と機械学習(通称PRML)」を読み進めながら、機械学習の理論面を一から勉強していく様子をお届けしたいと思います。

第9回目の今回は、前回（第8回）の続きでベイズ線形回帰を扱っていきます。まだ前回の記事を読まれていない方は、是非そちらを先にお読みいただきたいです。

▶　東大生AI初心者の学習日誌 Day8「ベイズ線形回帰（１）」

ベイズ線形回帰の目的（前回のおさらい）

ベイズ線形回帰を適用するシチュエーションについておさらいします。

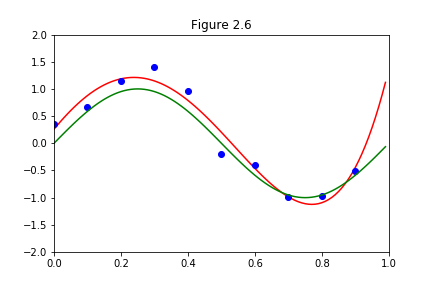
前回までの記事で、上の図の各点（青点）を近似する曲線を「多項式曲線フィッティング」にて求めた（赤線）ところ、そこそこの精度は出ることが分かりました。

しかし、データが少ないので、近似の精度が高い場所とそうでない場所があると考えます。それぞれの精度を確率分布として表そうと思った際に、ベイズ線形回帰が必要になってくるのでした。

具体的には、以下のようなイメージです。