こんにちは、じゅんペー(@jp_aiboom)です！

僕は現在東京大学の理系の二年生です。この連載では、AI初心者の僕が、「パターン認識と機械学習(通称PRML)」を読み進めながら機械学習の理論面を一から勉強していく様子をお届けしたいと思います。

第2回の記事では、既存のデータから未知のデータを予測する「回帰」を行うための手法である「多項式曲線フィッティング」を、実際にやりながら紹介しました。

第3回の今日は、前回に引き続き、多項式曲線フィッティングを例に回帰というテーマについてみていきます。さらに、機械学習をするときに、たびたび問題となる「過学習」についても触れていきます。

本記事の内容は前回の続きとなっておりますので、未読の方はまず第2回目の記事をご覧ください。

東大生AI初心者の学習日誌 Day2「多項式曲線フィッティング」

多項式曲線フィッティング

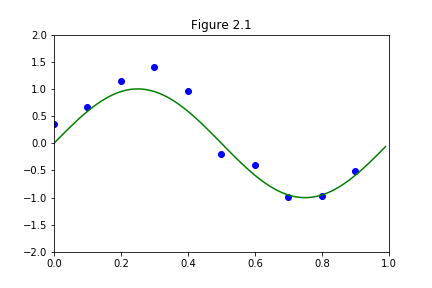
前回やっていたのは、上の図の青の点を用いて、できるだけ誤差が小さくなるように、緑のsin関数を近似したいという話でした。どんな関数で近似していくかというと、

$$y(x,\boldsymbol{w}) = w_0 + w_1x + w_2x^2 + … + w_Mx^M$$

この式で、自分で$M$を決め、どれだけ複雑な関数にするかが決まり、その後誤差が最小になるように$\boldsymbol{w}$を決めるのでした。そして、実際に$M=1$,$M=3$を計算してみると、以下のように近似曲線が引けるのでした。

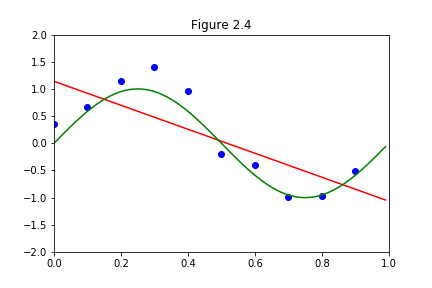
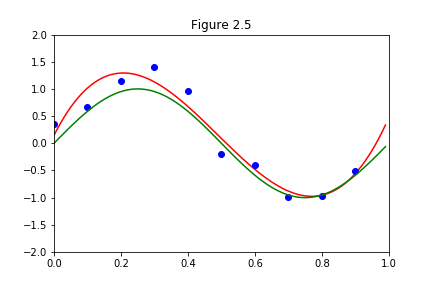
フィッティングの計算

前回の記事では、$M$を決めた後の $\boldsymbol{w}$の計算方法には触れていなかったので、簡単に解説していきます。

まず、$M$を決めたとしましょう。そのとき、近似曲線は、

$$y(x,\boldsymbol{w}) = w_0 + w_1x + w_2x^2 + … + w_Mx^M$$

この多項式で書かれるのでした。

上の例をみてもわかるように、この式は近似関数であって、完璧に10個の点を通過するわけではないので、それぞれの点において実際の縦軸の値とは誤差があります。誤差のイメージは下図です。

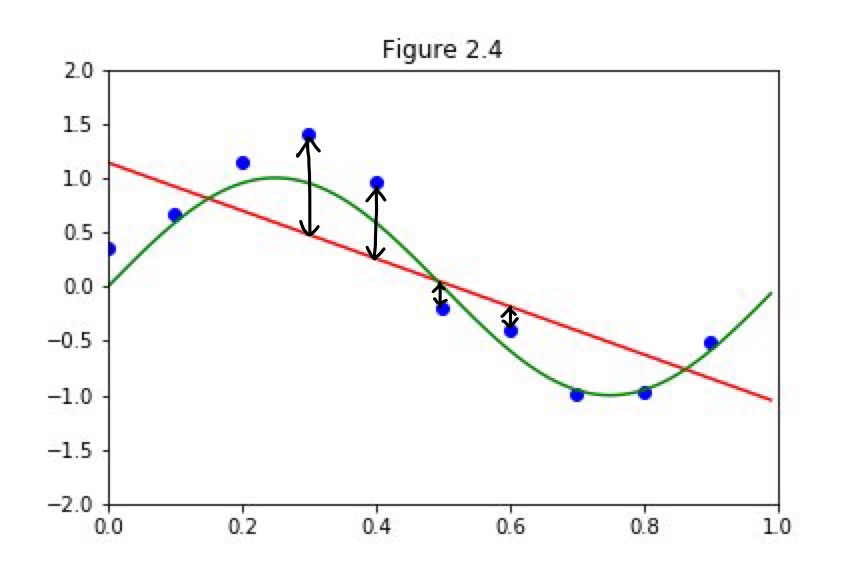
青の点の横軸の値を、$x_1,x_2,…,x_{10}$とすると、それぞれの点について誤差があるわけです。
それを式で表すと、
$$(i番目の誤差) = (t_i – y(x_i,\boldsymbol{w}))^2$$
とかけます。二乗しているのは、下にずれていても上にずれていても、ずれの絶対値の大きさで比べるためです。これが10個分あるので、
$$誤差の合計 = \sum_{i=1}^{10} (t_i – y(x_i,\boldsymbol{w}))^2$$
と表せます。これを最小化したいわけです。最小化なんて難しいように思えるかもしれませんが、実際はただの二次関数なので微分することで、簡単に$\boldsymbol{w}$を求めることができます。

過学習

ここまでで、どういう問題を解いているのかや、なぜ近似するのか、近似の計算の仕方が分かったと思います。ここからは、機械学習をする上でもっとも重要な事項の一つである「過学習」についてみていきたいと思います。